Cameron Race Time Prediction Formula and Calculator

Runners can estimate their time to finish a race based on the results of a previous race and one of several prediction formulas. A commonly applied model is Cameron's equation, which forecasts your next performance based on a previous race result. The equation is

T₂ = T₁⋅[D₂/D₁]⋅[f(D₁)/f(D₂)]

where T₁ is the previous time, D₁ is the distance previously run in meters, D₂ is the new distance to be run in meters, T₂ is the projected time for the new race, and the function f(x) is defined as

f(x) =
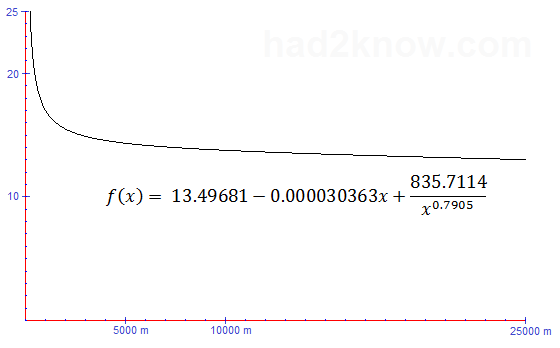
13.49681 - 0.000030363x + 835.7114/x^0.7905

The factor f(D₁)/f(D₂) has the effect of making your time increase by a slightly larger factor than the increase in distance. Equivalently, it makes your time decrease by a slightly smaller factor than the decrease in distance. A graph of f(x) is shown below along with an example computation.


You can use the calculator above to estimate your performance using Cameron's equation. To convert distances into meters, use the length conversion calculator.

Graph of f(x)

Example of How to Use the Cameron Equation

Last week, Tom ran 3.5 miles in 51 minutes and 30 seconds (5632.704 meters in 51.5 minutes). The week before, he ran 2.5 miles in 34 minutes and 45 seconds (4023.36 meters in 34.75 minutes). He wants to predict his time to run a 5-mile (8046.72-meter) race next week.

Using the Cameron formula on the first set of race results gives us

T₂ = 51.5(8046.72/5632.704)[f(5632.704)/f(8046.72)]
= 51.5*1.4285714*1.0212319
= 75.1334 minutes, or 1h 15m 8s

Using the Cameron formula on the second set of race results gives us

T₂ = 34.75(8046.72/4023.36)[f(4023.36)/f(8046.72)]
= 34.75*2*1.0445475
= 72.5961 minutes, or 1h 12m 35.76s

Averaging the two performance projections gives us (75.1334 + 72.5961)/2 = 73.86475 minutes, or 1h 13m 51.88s. Notice that this is close to the estimates obtained with the Riegel and VO2 Max performance prediction models.

© Had2Know 2010