How to Calculate Wire for Toroidal Coils

Determining the Maximum Number of Loops & Total Length of Wire

A toroid coil or toroidal inductor consists of torus (donut or ring shape) with wire looped around it. The magnetic torus is usually made of ferrite or iron powder, and may have either a rectangular cross-section (like a roll of duct tape) or a circular cross-section (like a donut). The wire is usually made of copper. Toroidal inductors and transformers are components of many electronics. They have several advantages over tube-wound coils (solenoid coils), the main benefit being their lower electromagnetic interference. Toroidal coils also cool down more quickly.

The length of wire needed to wind a toroidal coil depends on the inner radius of the torus, the outer radius, the cross-sectional shape, and the number of loops. The maximum number of non-overlapping loops that can be coiled depends on the inner radius of the torus and the radius of the wire. Below we discuss how to calculate the maximum number of loops that can be coiled on one layer, as well as how to compute the total length of wire needed for an arbitrary number of loops.

Determining the Maximum Number of Loops

The figure below shows a cross-sectional view of the inner radius of a toroid inductor and wire. The inner radius of the torus is A, the radius of the wire is r, and the maximum number of loops is n.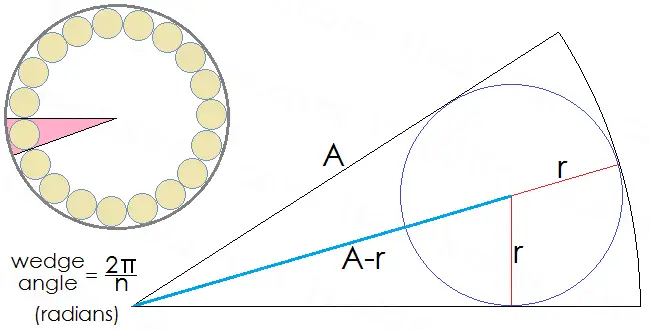

The equation that relates A, r, and n is

sin(pi/n) = r/(A-r) in radians.

If we use algebra to solve this equation for n, we arrive at

n = pi/[arcsin(r/(A-r))] in radians.

If you want to calculate in degree mode instead of radian mode, simply replace pi with 180. Here is an example to illustrate how to use this equation: Suppose the core of a toroidal inductor has an inner radius of 8 mm, and the wire has a diameter of 1 mm, i.e., a radius of 0.5 mm. Then the maximum number of coils that can be wound on a single layer is

n = pi/[arcsin(0.5/(8 - 0.5))]
= pi/[arcsin(1/15)]
= 47.0889.

So 47 loops can be wound around this torus with no overlap.

Calculating the Length of Wire (Circular Cross-Section)

If the toroidal coil has a circular cross-section, the then length of wire needed to wind the toroid inductor depends on the inner radius A, outer radius B, wire radius r, and number of loops n. The radius of the circular cross-section is (B-A)/2.

We can think of each loop as a spiral that goes around the shaft of a small cylinder from top to bottom. The radius of the cylinder is approximately (2r+B-A)/2, and the height is approximately (pi)(A+B)/n. Thus, each loop has length equal to

sqrt[ (pi(2r+B-A))² + (pi(A+B)/n)² ]
= (pi)sqrt[ (2r+B-A)² + ((A+B)/n)² ].

Since there are n loops, the total length is approximately

(pi)(n)sqrt[ (2r+B-A)² + ((A+B)/n)² ]
= (pi)sqrt[ (n(2r+B-A))² + (A+B)² ].

For example, suppose we have wire with a radius of 0.5 mm, a torus with an inner radius of 10 mm and an outer radius of 30 mm, and we make a toroidal coil with 45 loops. We have r = 0.5, A = 10, B = 30, and n = 45. Then the total length of wire needed is

(pi)sqrt[ (45(1+30-10))² + (10+30)² ]
= (pi)sqrt[ (945)² + (40)² ]
= (pi)sqrt[ 894625 ]
= 2971.5 mm, or 2.9715 meters.

Calculating the Length of Wire (Rectangular Cross-Section)

When a toroidal inductor has a rectangular cross-section, the length of wire depends on the inner radius A, outer radius B, torus height H, wire radius r, and number of loops n. The length of wire needed to wrap one loop of the coil is approximately

sqrt[ (4r+2H+2B-2A)² + (pi(A+B)/n)² ].

The total length of wire needed is

sqrt[ (n(4r+2H+2B-2A))² + (pi(A+B))² ].

© Had2Know 2010