Hollow Rectangular Beam Calculator

Moments and Bending Moments of Inertia, Area, Mass

Builders use hollow rectangular beams in construction because such beams can withstand the forces of shearing and bending in both the x- and y-directions. They are also resistant to torsional forces, much more so than I-beams. To calculate strains on hollow square/rectangular beams, you must know the cross-sectional area and various moments of inertia in both the x- and y-directions. You can use either the calculator or the formulas below.

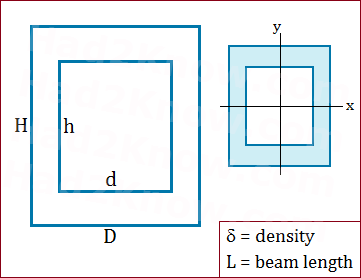
Using the above diagram as a guide, enter the dimensions of the beam into the calculator. D is the outer width of the rectangle, d is the width of hole, H is the outer height of the rectangle, and h is height of the hole. L is the total length of the beam and δ is the density.

Enter the measurements in centimeters and the density in kg/cm³. Use the fact that 1 cm = 0.01 meter and 1 grams = 0.001 kg, or use the conversion calculator if necessary.

Area, Volume, Mass Equations

The cross-sectional area of a hollow beam is calculated by subtracting the area of the inner rectangle from the outer rectangle. Beam volume is area times length. Beam mass is density times volume. Accordingly, the three formulas are

Area = HD - hd
Volume = (HD - hd)L
Mass = (HD - hd)Lδ

Moments of Inertia

The moment of inertia measures an object's resistance to being rotated about an axis. (Not to be confused with the second moment of inertia described in the next section.) When the axis passes through the centroid in the x-direction or y-direction, the moment equations are

I_X = (δ⋅HDL)(H² + L²)/12 - (δ⋅hdL)(h² + L²)/12
I_Y = (δ⋅HDL)(D² + L²)/12 - (δ⋅hdL)(d² + L²)/12

These are derived by subtracting the moment of inertia of the solid inner rectangular beam from the m.o.i. of the solid outer beam. To calculate the m.o.i. about an axis that is parallel to one of the centroidal axes, use the Parallel Axis Theorem:

I_N = I_C + mr²

where I_N is the new moment of inertia about the line N, I_C is a centroidal moment of inertia, m is the mass, and r is the distance between axes.

Bending Moments of Inertia (Second Moment of Inertia)

The second moment of inertia, also known as the bending moment or area moment of inertia, is expressed in cm⁴. This should not be confused with the usual moment of inertia explained above. Among beams with the same cross-sectional area but different shapes, hollow beams have higher bending moments in both the x- and y-directions, which means they are good at resisting shearing and bending side to side and top to bottom. The bending moments in the x- and y-directions passing through the centroid of the beam are

I_X-area = H³D/12 - h³d/12
I_Y-area = D³H/12 - d³h/12

To find the area moment of inertia with respect to an axis that is parallel to a centroidal axis, there is an area version of the Parallel Axis Theorem:

I_N-area = I_C-area + Ar²

where A is the cross-sectional area.

Solid Rectangle

To calculate the moments, area, volume, and mass of a solid rectangular beam, just set d = h = 0.

© Had2Know 2010