Factors That Affect the Minimum Bending Radii of Pipes, Cables, and Sheet Metal

In engineering, the minimum bending radius of a material tells you how tightly a piece can be bent before it breaks. Materials that can withstand a high degree of curvature are preferred in construction because they are more versatile, lending themselves to a wider array of industrial applications

Many factors affect a material's minimum bending radius, and knowing these factors is crucial to building sound structures. For example, engineers who lay fiber optic cables often need to wind the cable around cylinders. Winding too tightly can damage the wires. In pipe fitting and sheet metal construction, the minimum bending radii of materials depends on their thickness, composition, and skill of the machinist.

How Minimum Bending Radius is Measured

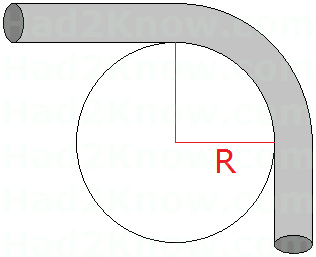
The bending radius of a metal tube (or cable or piece of sheet metal) is defined as the radius of the inner part of the curve. If you coil a pipe around a cylinder that has a 24 inch diameter, then the bend radius is 12. The minimum bending radius, R, is the radius of the smallest such cylinder that a pipe can be bent around.

There is no single formula for calculating the minimum bending radius of tubing or sheet metal because there are too many variables to consider, not the least of which is the machinist's skill level and technique. (See rules of thumb for sheet metal's bending radius.) However, the following list describes the main limiting factors in how tightly a sheet, pipe, or cable can be coiled.

Outer Diameter of Pipe or Thickness of Sheet

The wider the pipe/tube or the thicker the piece of sheet metal, the larger the minimum bending radius. Materials that are too thick or wide overall cannot be bent as compactly as materials that are thinner overall.

Thickness of Tube Walls

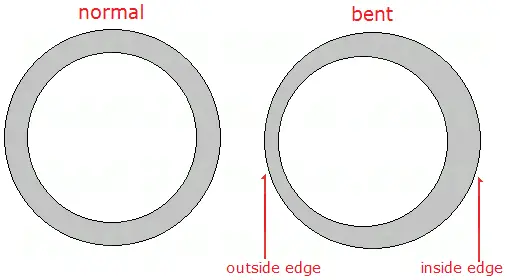
The thicker the tube wall, the smaller the minimum bending radius. When tubing is bent, the wall of the outside edge of the curve stretches and becomes thinner, while the wall of the inside edge compresses and becomes thicker. If the walls of tubing are too thin to begin with, the outside edge will break, kink, or deform.
Ductility

The more ductile the material, the smaller the minimum bending radius. Rubber, as well as annealed and untempered metals can be wound around smaller cylinders. Harder materials cannot be bent as tightly.

Corrugation

A corrugated pipe has a smaller minimum bending radius than a smooth pipe made of the same material with the same dimensions. Manufacturers form stainless steel into corrugated pipes to gain flexibility while still retaining the strength of steel.

Bending Techniques

• Sheet Metal: Machinists bend sheet metal using a V-shaped punch and die. Because sheet metal is solid and thinner than pipes, it tolerates more extreme curvature when bent. It is easier to bend sheet metal parallel to the grain, but this also increases the likelihood of cracking.
  
  Here are three rules of thumb for figuring the minimum bending radius of sheet metal. For the most accurate numbers, you should always check with the manufacturer since they perform actual tests to see how far the metal can be bent.
  
  
  1. theoretical minimum bending radius = thickness of the sheet
  2. safer minimum bending radius = four times the thickness of the sheet
  3. m.b.r. = T(100-E)/(2E), where T is the thickness and E is the % elongation at break. For example, suppose a sheet is 5 mm thick and its ductile strength permits 25% elongation before breaking. Then the minimum bend radius is about 5(100-25)/(2*25) = 7.5 mm.



• Pipes and Tubing: Bending pipes and tubes is more challenging and requires more tools to make a clean, wrinkle-free bend. A clamp die stabilizes the outer wall of the pipe while the bend die is used to form the crotch of the curve. Mandrels and ball bearings are inserted into the tube to keep the walls from collapsing while the tube is bent. A wiper die wedges between the tube and the bending die to "wipe" away the crinkles that may form on the inner part of the bend.

© Had2Know 2010