Refraction Index Calculator

In optics, the refractive index of a transparent material is a number that indicates how light and radiation travels and propagates through the medium. If a material has a refractive index of n, the wavelength and the velocity of the radiation are reduced by a factor of n with respect to the vacuum values of wavelength and velocity. For a vacuum, n = 1 by definition; for all other media with normal physical properties, n > 1.

If you know the focal length of a lens, the radii of curvature of both sides, and the lens thickness, then you can solve for the index of refraction using the lensmaker's equation

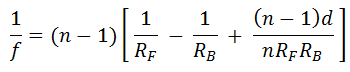
where f is the focal distance, R_F is the front radius, R_B is the back radius, and d is the lens thickness.

Focal Distance Diagram

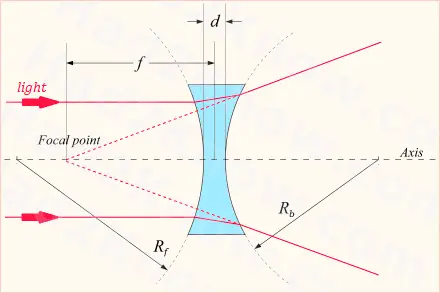
The diagram above shows the location of the focal point of the lens for a biconcave lens. If the focal point is on the same side as the light source, the focal distance is negative and the lens is divergent. If the focal point is behind the lens the focal length is positive and the lens is convergent. If the focal length is infinite, the lens has no power and is neither divergent nor convergent.

Types of Lenses and Their R_F and R_B Values

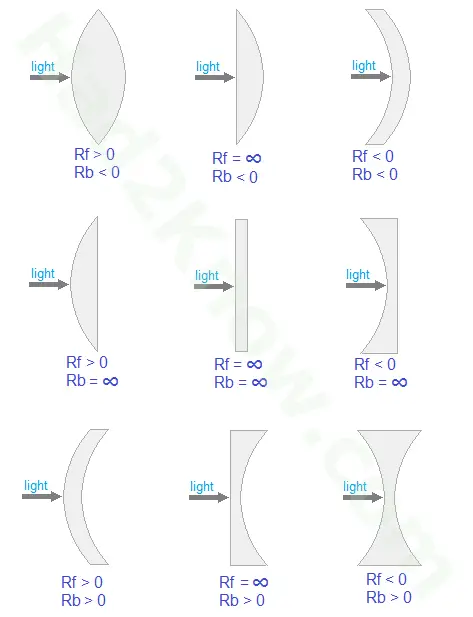
When plugging the values of R_F and R_B into the focal length equation, sign matters! If the center of curvature is away from light source, the radius is positive. If the center of curvature is near light source, the radius is negative. If either side is flat, the radius is infinite and the value of 1/R is 0.

Example

A bi-concave lens has a focal length of -300 cm and a thickness of 0.3 cm. The radius of curvature of either side is 435 cm. The values of the key variables are

R_F = -435
R_B = 435
d = 0.3
f = -300

The refractive index can be found by solving the following equation for n:

-1/300 = (n-1)[-1/435 - 1/435 + (n-1)*0.4/(n*435*435)]

Simplifying this equation yields

an² + bn + c = 0

where a = 2/435 - 0.3/435², b = 0.6/435² - 2/435 - 1/300, and c = -0.3/435². Solving this equation using the quadratic formula yields one solution less than 1 and one solution greater than 1. Since only the latter makes physical sense in the context of optics, the solution is n = 1.724895.

© Had2Know 2010