How to Calculate the Thickness of a Rolled Sheet

When you roll a sheet of any thin, pliable material, it will form the shape of a cylindrical tube. If you know the cylinder's dimensions and the total length of the rolled material, you can compute the sheet's thickness using geometry.

(Similarly, if you know the measurements of the tube and the thickness of the material, you can find the length. See companion article.)

The cross-sectional shape of the rolled tube is an annulus. When the sheet is laid flat, the cross-sectional shape is a long rectangle. The areas of these two shapes are equal, a convenient fact that allows you to solve for the thickness.

See the diagram below:

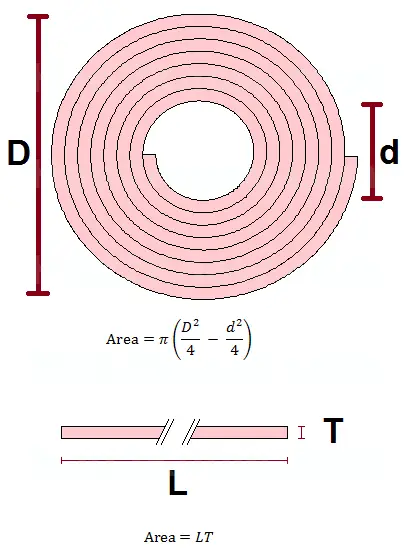
If the outer diameter of the rolled material is denoted by D, the inner diameter by d, the thickness of the material by T, and the length by L, then the four variables are related by the equation:

π[D²/4 - d²/4] = LT

The expression on the left is the area of the annulus and the expression on the right is the area of the rectangle. You solve for T by dividing both sides of the equation by L. This gives you

π[D²/4 - d²/4]/L = T

This is the equation for the thickness of a rolled sheet in terms of its length and the cylinder's outer and inner diameters. When using this formula, make sure that each quantity is measured in the same units.

Example

Suppose a sheet of flexible material is rolled into a cylinder that has an outer diameter of 13 inches and an inner diameter of 2 inches. If the sheet is known to be 415 feet long, how thick is the material?

The quantities given in the problem are D = 13, d = 2, and L = 415*12 = 4980, where each measurement is in inches. Now you can compute T with the formula above:

T = π[D²/4 - d²/4]/L
= π[13²/4 - 2²/4]/4980
= π[41.25]/4980
= 0.026022 inches, or about 0.661 mm.

© Had2Know 2010