Angle and Radius of an Arc

An arc is a section of a circle's circumference; it can span just a tiny segment of the circumference, or a much greater portion of the circle's border. One of the most commonly encountered geometric problems involving arcs is determining the radius of a circle that contains a given arc. A related problem in trigonometry is to find the angle of the sector defined by the arc.

Such math problems can arise in manufacturing, design, landscaping, or any kind of construction based on circles. Luckily, it is very easy to find both the radius and the angle of a circular arc as long as you know its height and base length. You can apply the geometry and trig formulas with diagrams below, or use the convenient arc calculator on the left.

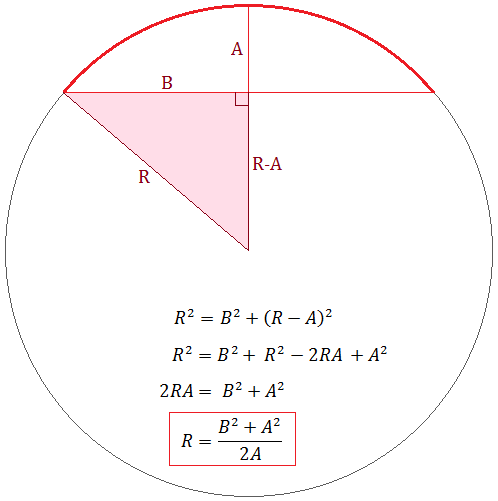
How to Solve for the Radius

Using the Pythagorean theorem, you can solve for R by setting up an equation that involves the arc height A and half the base length B. As shown in the figure below, one leg of the right triangle has length B, and the other has length R-A.

The Pythagorean theorem gives the equation R² = B² + (R-A)², which has the unique solution of R = (A²+B²)/(2A). No trig is required to solve this problem, just algebra.

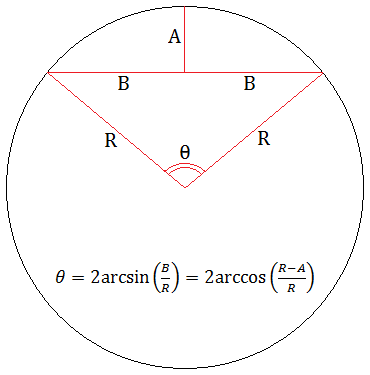
How to Solve for the Angle

If the angle of the arc is θ, then you can relate θ/2 with R and B by the equation

sin(θ/2) = B/R
θ/2 = arcsin(B/R)
θ = 2arcsin(B/R), or alternatively θ = 2arccos((R-A)/R)

These equivalent solutions come from the definitions of sine and cosine: sine equals opposite over hypotenuse, and cosine equals adjacent over hypotenuse.

Example Calculation

An arc measures 3 cm high and 14 cm across, what is the radius of the circle that contains this arc, and what is the angle?

The problem gives us A = 3 and B = 14/2 = 7. So we have

R = (3² + 7²)/(2*3)
= 58/6
= 9.6667 or 9 ²/₃

θ = 2arcsin(7/(58/6))
= 2arcsin(21/29)
= 92.79°

© Had2Know 2010