Beta Function Calculator

The beta function B(x, y) can be defined in terms of the Gamma Function or several integrals. The standard formula is

B(x, y) = Γ(x)Γ(y)/Γ(x+y),

and if x and y are positive integers the formula is

B(x, y) = (x-1)!(y-1)!/(x+y-1)!

Like the gamma function, the beta function can have complex arguments and is undefined at 0 and negative integers. The beta function arises in the evaluation of certain integrals. For example,

B(n, m) = ∫¹_o u^n-1(1-u)^m-1 du

B(n, m) = ∫^∞_o u^n-1(1+u)^-n-m du

B(n, m) = 2∫^π/2_o   cos^2n-1(u) sin^2m-1(u) du

Properties of the Beta Function

The beta function is symmetric, meaning B(x, y) = B(y, x). In each of the integral formulas above, you can interchange n and m without changing the value of the integral. Some other properties and formulas involving the beta function are: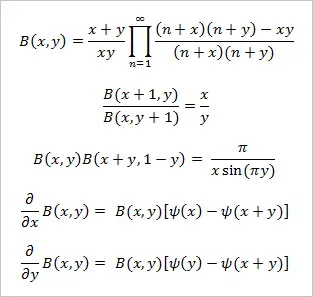 The function ψ(z) is the Digamma Function.

Uses of the Beta Function

The beta function appears as a constant in the beta distribution, a probability density function defined over the interval [0, 1] by the equation

p(x) = (1/B(n, m))x^n-1(1-x)^m-1.

The beta distribution is applied in situations where the domain is bounded, for example, in predicting the duration of projects and tasks. Some mathematical tools used in project management are derived from the beta distribution. The mean and variance of the beta distribution are

μ = n/(n+m)
σ² = nm/[(n+m)²(n+m+1)]

© Had2Know 2010