Cone Construction Calculator

A cone is constructed by taking a circle sector of radius L and angle θ and joining the two straight edges together. And any cone without a closed base can be formed back into a circle sector by cutting a straight line from the nape to the base and flattening the resulting figure.

If you are given L and θ, you can plug these values into equations to find the height (H) and base radius (R) of the corresponding cone. Likewise, if you are given H and R, you can plug these values into equations to find L and θ. These formulas are explained below the diagrams.

You can also use the convenient calculator on the left to find H and R or L and θ. Just enter the measurements in the appropriate column and click the corresponding button to compute.

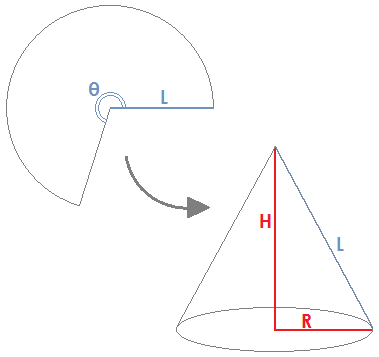
Figuring L and θ Given H and R

The relation among L, H, and R comes from the Pythagorean Theorem: H² + R² = L², or equivalently, L = sqrt(H² + R²).

To find θ given H and R, note first that the circumference of the cone's base is 2πR, which is also the arc length of the flattened sector. The circumference of the larger circle from which the sector is cut is 2πL. A sector's angle is equal to 360° times the ratio of the arc length to the full circumference. Thus, θ = 360R/L, or equivalently, θ = 360R/sqrt(H² + R²).

Figuring H and R Given L and θ

The equations for L and θ above can be manipulated to solve for H and R. First, notice that

Lθ = sqrt(H² + R²)*360R/sqrt(H² + R²) = 360R,

Thus, R = Lθ/360. If you substitute this expression for R into the equation L = sqrt(H² + R²), you can solve for H in terms of L and θ. This gives you

H = L*sqrt[1 - (θ/360)²]

Example

A circular sector has a radius of 10 cm and an angle of 210°. If the figure is formed into a cone, what will its height and base radius be? First we have L = 10 and θ = 210. Using the equations for H and R gives us

R = 10*210/360 = 5.8333 cm

H = 10*sqrt[1 - (210/360)²] = 8.1223 cm

© Had2Know 2010