Equation of a Cubic Through 4 Points

If you have four distinct points in the xy-plane, and no two x-coordinates are equal, then there is a unique cubic equation of the form

y = ax³ + bx² + cx + d

that passes through the four points. You can use matrix algebra to find the coefficients a, b, c, and d, or you can use the convenient calculator on the left. The matrix method of solving this problem is explained below, and a graphing calculator can be used to quickly compute matrix operations.

The Matrix Method

To solve for the coefficients a, b, c, and d, you must set up and solve a matrix equation Ax = B, where A is a 4-by-4 matrix, x is a 4-by-1 matrix of the undetermined coefficients, and B is a 4-by-1 matrix.

The entries of matrix A are determined by the x-coordinates of the pairs (x₁, y₁), (x₂, y₂), (x₃, y₃), and (x₄, y₄). The expression is The entries of matrix B are the y-coordinates of the pairs (x₁, y₁), (x₂, y₂), (x₃, y₃), and (x₄, y₄). Thus, the full matrix equation is The solution to this matrix equation is x = A^-1B. As long as all of the x values are distinct, matrix A will be invertible, thus, there will be a unique solution set for a, b, c, and d.


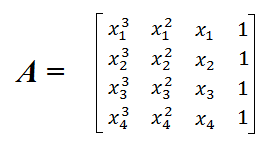
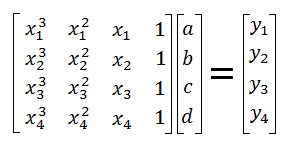
Example

John has a rectangular box with a volume of 40. When he increases each side length by 1 unit, the volume increases to 90. When he increases the sides by 2 units, the volume increases to 168. If he reduces each side by 1 unit, the volume shrinks to 12. Find a function f(x) that gives the volume of the box when the sides are increased by x units.

The four data points are (0, 40), (1, 90), (2, 168), and (-1, 12). Plugging these values into the calculator or matrix equation gives us

a = 1, b = 11, c = 38, and d = 40.

The equation is f(x) = x³ + 11x² + 38x + 40.

© Had2Know 2010