Gini Coefficient Calculator

The Gini coefficient, named after Italian statistician Corrado Gini, is a dimensionless measure of statistical dispersion that is frequently used in the analysis of income distribution.

The Gini coefficient, G, of a data set or income distribution curve ranges from 0 to 1, with 1 being the most unequal distribution of wealth (one person owns everything) and 0 being the most equal (each person owns an equal share).

Mathematically, G is the ratio of the area between the wealth distribution curve (Lorenz curve) and the line of equal distribution (straight line) to the area under the equal distribution curve. This is best described graphically:

        

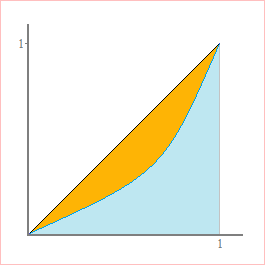
Computing the Gini Coefficient (Empirical Distribution)

For an empirical Lorenz curve, one generated by discrete data points, you can compute the Gini coefficient with the formula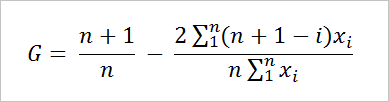

where the x_i are ordered from least to greatest. For example, suppose $12 is distributed among five people as follows: two people receive $3 and three people receive $2. In this scenario,

the bottom 20% own $2, or 16.7% of the wealth
the bottom 40% own $4, or 33.3% of the wealth
the bottom 60% own $6, or 50% of the wealth
the bottom 80% own $9, or 75% of the wealth
the bottom 100% own $12, or 100% of the wealth

The Lorenz curve is

and the Gini coefficient is

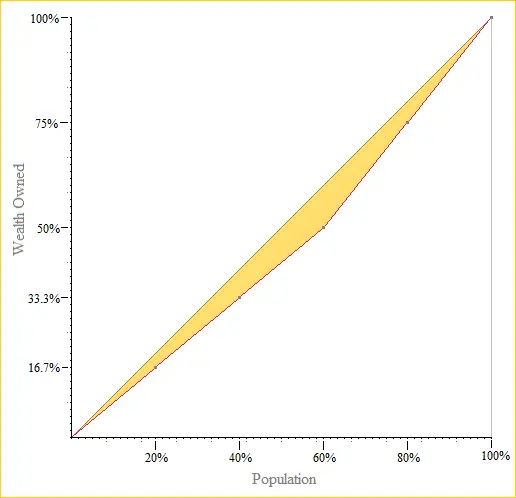
6/5 - (2*33)/(5*12) = 1.2 -1.1 = 0.1

Computing the Gini Coefficient (Theoretic Distribution)

If the Lorenz curve is given by a function f(x) over the interval [0, 1], then the Gini coefficient can be found with integration. The formula is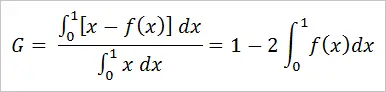

For example, if the Lorenz curve is g(z) = 0.25z4^z, then the Gini coefficient is 0.33782.

© Had2Know 2010