Hexagonal Circle Packing Within a Rectangle
Hexagonal Circle Packing Calculator
When packing circular objects in a box, the densest way to pack is with a hexagonal arrangement, as shown in the image below.
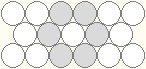
For example, if you pack identical cylindrical cans in a rectangular box, it might seem more natural to place them in a rectangular (square) array. However, if you have enough cans, packing them hexagonally can reduce both the area and the perimeter of the surrounding rectangle, even if there are large gaps at the ends of the rows.
The calculator below computes the perimeters and areas of various rectangles that will contain a given number of circles in a hexagonal arrangement. It allows you to compare hexagonal and rectangular packing side by side, so you can find the optimal solution that minimizes space. The formulas for computing the area and perimeter of a hexagonal arrangement are described below.
For instance, suppose you need to pack 18 cans in a rectangular box. If you pack them in square formation, you can make 6 rows of 3, or 9 rows of 2. The first option yields a rectangle with perimeter = 18 and area = 18. The second option yields a rectangle with perimeter = 22 and area = 18.
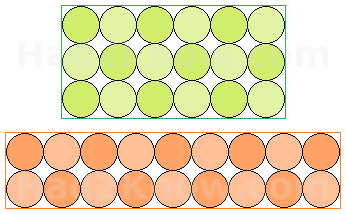
However, in the figure below, you can see five ways to pack 18 cans in a hexagon formation:
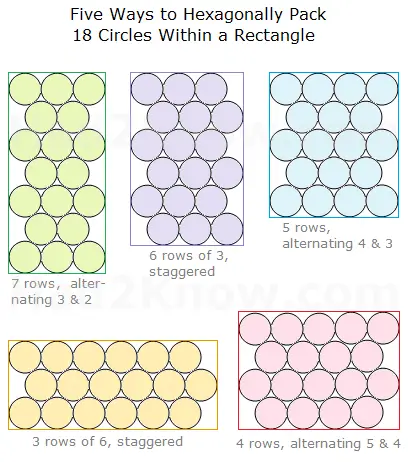
The respective perimeters and areas of the surrounding rectangles are:
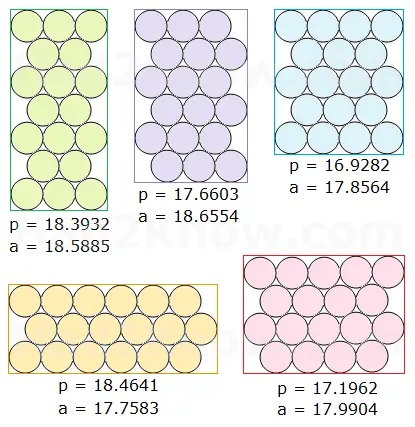
As you can see, if you arrange the cans in 5 rows, alternating 4-3-4-3-4, you will achieve a smaller perimeter and area than with either of the two rectangular packing arrangements. This helps reduce the amount of shipping materials needed.
If you have a hexagonal arrangement with k rows of alternating length, in which the length of the longest row is n, then
perimeter = 2n + √3k + 2 - √3
area = n[(√3/2)k + 1 - √3/2]
If you have a hexagonal arrangement with k rows of equal length n (aka staggered), then
perimeter = 2n + √3k + 3 - √3
area = (n + 1/2)[(√3/2)k + 1 - √3/2]
(Both formulas assume the diameter of each circle is 1. If the diameter is d, multiply the perimeter formula by d and the area formula by d².)
© Had2Know 2010
