Integer Partition Function Calculator

Integer partitions count the number of ways a positive integer n can be written as the sum of positive integers less than or equal to n, ignoring the order of summands.

The integer partition function is often denoted by P(n). For example, P(7) = 15 because there are 15 ways to write 7 as a sum:



7
6+1
5+2
4+3
5+1+1
4+2+1
3+3+1
3+2+2
4+1+1+1
3+2+1+1
2+2+2+1
3+1+1+1+1
2+2+1+1+1
2+1+1+1+1+1
1+1+1+1+1+1+1

Properties of P(n)

For mathematical convenience, P(0) is defined as 1. While there is no simple explicit formula for computing P(n), there is a recursion formula that allows you to calculate P(n) as long as you know the values of P(i) for i < n. The recursive formula is

P(n) = Σ (-1)^k+1[P(n - k(3k-1)/2) + P(n - k(3k+1)/2)],

where k ranges from 1 to n. Because P(b) = 0 for all negative integers b, many of the terms in this series vanish. As an example, let's use the above formula to compute P(13) and P(15).

P(13) = P(13-1) + P(13-2) - P(13-5) - P(13-7) + P(13-12) + P(13-15) - ...
= P(12) + P(11) - P(8) - P(6) + P(1) + P(-2) - ...
= 77 + 56 - 22 - 11 + 1 + 0 - ....
= 101.

P(15) = P(15-1) + P(15-2) - P(15-5) - P(15-7) + P(15-12) + P(15-15) - ...
= P(14) + P(13) - P(10) - P(8) + P(3) + P(0) - ...
= 135 + 101 - 42 - 22 + 3 + 1 - ....
= 176.

This is sometimes known as the pentagonal number recursion formula since numbers of the form k(3k-1)/2 and k(3k+1)/2 are generalized pentagonal numbers.

Another recursive formula for the integer partition function is

nP(n) = Σ σ₁(n-k)P(k),

where k = 0,...,n-1 and σ₁ is the divisor function. As another example, we can use this formula to compute P(7).

7P(7) =

σ₁(7)P(0)+ σ₁(6)P(1) + σ₁(5)P(2) + σ₁(4)P(3) + σ₁(3)P(4) +σ₁(2)P(5) + σ₁(1)P(6)

= 8*1 + 12*1 + 6*2 + 7*3 + 4*5 + 3*7 + 1*11
= 8 + 12 + 12 + 21 + 20 + 21 + 11
= 105

Since 7P(7) = 105, P(7) = 105/7 = 15.

Asymptotic Formula

For large values of n, P(n) can be approximated with the asymptotic formula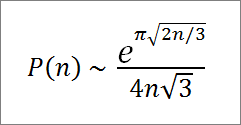



For example, the exact value of P(200) is 3,972,999,029,388. With the asymptotic formula, the approximate value is

e^36.2759873/1385.6406461 = 4,100,251,494,852.9.

© Had2Know 2010