Folding a Rectangular Box of Maximal Volume (Flapped Lid)

You can quickly construct a box with a flapped lid by cutting and folding a sheet of rectangular paper, cardstock, or cardboard. The basic idea is to cut six equal squares from the corners and sides of the paper to create flaps, which are then folded upward and taped together to form the sides of the box.

(A detailed pattern with instructions for making such a box is described in the Had2Know article "How to Fold a Rectangular Box with a Lid.")

By varying the size of the squares you cut away from the sheet, you can end up with boxes of various shapes and sizes. This article describes how to determine the optimal square size to cut so that your box has the maximum possible volume.

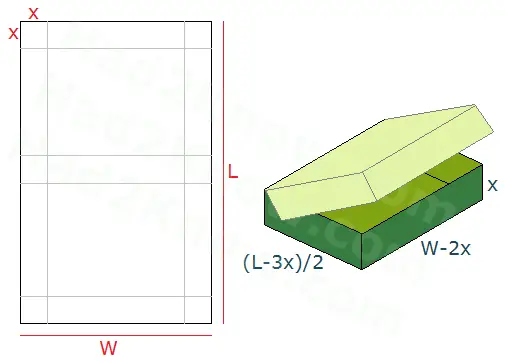
Suppose you begin with a rectangular sheet of paper with length L and width W. Let X be the side length of the squares cut out from the corners and sides. After you cut out the squares and fold the box according to the pattern, the resulting box will have a height of X, a width of W-2X, and a length of (L-3X)/2. See image above.

The volume V is X(W-2X)(L-3X)/2. To find the maximum volume, we take the derivative of V(X) = X(W-2X)(L-3X)/2, set it equal to zero, and solve for X. Here we assume that L and W are given constants, so our solution for X will be in terms of L and W.

V(X) = X(W-2X)(L-3X)/2
V(X) = 3X³ - (L+1.5W)X² + (LW/2)X
V'(X) = 9X² - (2L+3W)X + LW/2

9X² - (2L+3W)X + LW/2 = 0
X = [2L + 3W ± sqrt((2L+3W)² - 18LW)]/18
X = [2L + 3W ± sqrt(4L² - 6LW + 9W²)]/18
X = L/9 + W/6 ± sqrt(4L² - 6LW + 9W²)/18

The only solution that yields a constructable box is
X = L/9 + W/6 - sqrt(4L² - 6LW + 9W²)/18

Example: Suppose a rectangular sheet of cardboard is 24 inches long and 10 wide. To find the optimal size of square to cut away from the corners, we plug L = 24 and W = 10 into the equation

X = L/9 + W/6 - sqrt(4L² - 6LW + 9W²)/18.

This gives us

X = 24/9 + 10/6 - sqrt(2304 - 1440 + 900)/18
= 8/3 + 5/3 - sqrt(1764)/18
= 8/3 + 5/3 - 42/18
= 2

This means you should cut 2 by 2 squares from the corners and sides of the cardboard to build a box with maximal volume. The box will be 2 inches high, 6 inches wide, and 9 inches long, yielding a volume of 108 cubic inches.

© Had2Know 2010