How to Fold a Rectangular Box with a Lid

If you have stiff paper and tape or glue, you can quickly construct a sturdy rectangular box with a lid flap. Just use a pencil, ruler, and scissors to make the pattern described in the steps below, glue the tabs in place, and in less than 10 minutes you will have a simple storage box. You can use the box to hold light-weight odds if you construct it from paper or cardstock. Or you can make gift boxes or shipping containers out of heavier cardboard.

(Step 1) Use a ruler and pencil to draw a frame inside the rectangular sheet. The frame must have the same width all around the perimeter, creating perfect squares at the corners. You can make the frame any size you wish; keep in mind that the width of the frame will determine the height of the box. Drawing a wide frame will result in a deep box with a small base. Drawing a thin frame will result in a shallow box with a large base.

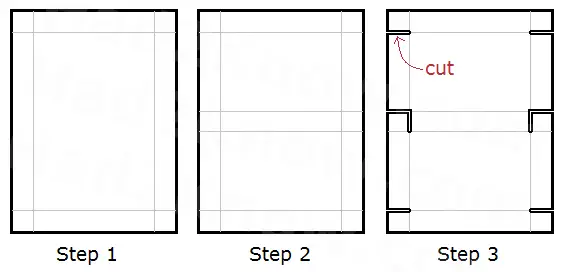
(Step 2) Now split the frame in half by drawing a bar that is as wide as the frame. Be sure to center it properly so that the top and bottom halves are equal. This will create two more little squares, one on each side of the sheet.

(Step 3) The six small squares form the tabs that are glued to the sides of the box, giving it a 3-dimensional shape. Cut along the lines as shown in the figure above. Do not cut any farther than the lines indicate.
(Step 4) Fold upward along the gray pencil lines so that the figure curls into itself. Then, using the red dots and arrows as a guide, glue the tabs so that adjacent dots overlap. The top part of the figure will become the lid and the bottom part will become the base of the box.

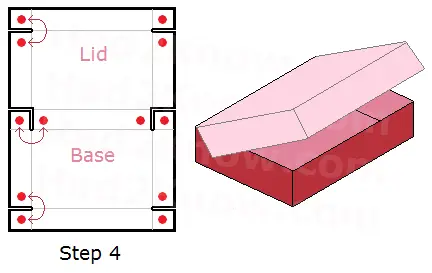
If you want to construct such a box with the largest possible volume, you can use calculus to determine the width of the frame that will yield a box with maximum volume. The Had2Know article "Folding a Rectangular Box of Maximal Volume (Flapped Lid)" shows the math and the final answer. It also has a convenient calculator for computing the optimal dimensions.

© Had2Know 2010