3 Variable Power Regression:
z = ax^by^c

Using Least Squares Regression to Fit a Power Function z = ax^by^c

The least squares multiple linear regression method can be used to find a curved surface that best fits a given set of sample data. If you select a power model of the form z = ax^by^c, you are in luck since this equation can be linearized:

z = ax^by^c
ln(z) = ln(ax^by^c)
ln(z) = ln(a) + b*ln(x) + c*ln(y)

This equation is linear in the undetermined coefficients ln(a), b, and c, as well as in the transformed variables ln(z), ln(x), and ln(y). You can use the same technique as in simple multiple linear regression to solve for ln(a), b, and c.

The matrix equation for this model is


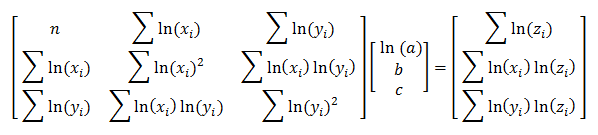
Once you find the value of ln(a), you can find the value of a with the relation a = e^ln(a).

Example

A city planning official wants to find a tri-variate power function that predicts the length of construction projects based on the square footage of the finished building and the number of construction workers. The form of the function is

z = ax^by^c

where z is the duration of the construction in days, x is the square footage of the finished building, and y is the number of workers. She uses the following historical(x, y, z) data:

(10000, 50, 62)   (15000, 120, 45)   (10500, 78, 40)
(25000, 40, 124)   (18000, 85, 68)   (19000, 80, 90)

Using the three-variable power regression calculator above, the equation of the surface is

z = 0.2247(x^0.8392)(y^-0.5646)
= 0.2247x^0.8392/y^0.5646

The exponents in this equation make sense in a practical context. The exponent of x should be positive since we expect a larger building to require more time. The exponent of y should be negative (y in the denominator) since the construction time is reduced by adding more workers to the project.

If the official wants to use this equation to estimate the duration of a 16500 sq.ft. building project with 95 workers, she must plug x = 16500 and y = 95 into the equation. This produces

z = 0.2247(16500^0.8392)/95^0.5646
= 59.4693 days.

Compare this answer to the answer obtained with simple multiple linear regression. Another model that may be appropriate is the three-variable exponential regression model.

© Had2Know 2010