Δ Side, Angle, & Area Calculator

Triangular laws of congruence state that two triangles are equivalent if they have the same values for side-angle-side (SAS), angle-side-angle (ASA), or side-side-side. It follows that if you know the SAS, ASA, or SSS values for a triangle, you can compute the missing sides and angles, as well as the area!

The calculator below computes the area and unknown angles and sides of a triangle if you input (i) two sides and the angle between--SAS, (ii) two angles and the side between--ASA, or (iii) all three side lengths--SSS.

Pick One
SAS side = angle = o side =	ASA angle = o side = angle = o	SSS side = side = side =

How the Calculator Works

The calculator uses standard geometry and trig formulas. You can find the equations for triangular area in the related article, "How to Compute the Area of a Triangle: SSS, SAS, ASA, Base Height." The formulas for computing missing angles and side lengths can be found in the Trig and Angles Formula Sheet.

Why Not AAS or SSA?

You may wonder why there are no options for AAS (two adjacent angles and a side length not between the angles) or SSA (two adjacent sides and an angle not between the sides).

The first option, AAS, is actually equivalent to ASA. Why? Because if you know two angles of a triangle, you automatically know the third angle since all three must add up to 180. Thus, you can identify the triangle by the side length and the two angles on either side.

The second option, SSA, does not uniquely identify a triangle, except when the angle is equal to 90°. Here is an example that shows two incongruent triangles with the same values for SSA:

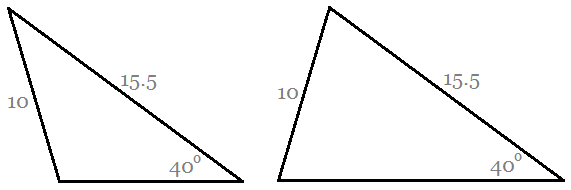
© Had2Know 2010