Radius of a Circle Tangent to Two Circles and Inside Another Tangent Circle

If you have two circles that are tangent to each other and circumscribed by another tangent circle, you can find a fourth circle that is also inside the larger circle and tangent to the other three, forming a set of four mutually tangent circles. This is known as the Soddy Circle Problem.

In this problem, there are two possible solutions for the additional circle. In the figure below, the gray circles are given and the pink circles represent the two solutions for fourth tangent circle.

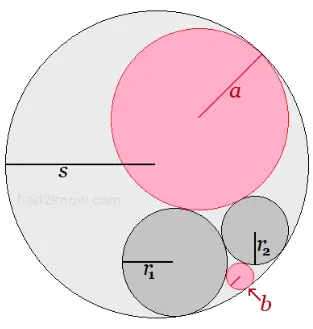
To use the calculator on the left, input the radii of the three tangent circles and click to find the radii of the fourth tangent circles. An explanation of Descartes' Theorem is given below.

Descartes' Theorem When Two Tangent Circles are Inside a Third

Suppose two circles are tangent to each other and inside of another circle, also tangent. Let the radii of the interior circles be A and B and the radius of the outer circle be C. If X is the radius of a fourth tangent circle inside the diagram, then the relation among A, B, C, and X is

[1/A + 1/B - 1/C + 1/X]² = 2[1/A² + 1/B² + 1/C² + 1/X²]

Solving this equation for X yields two solutions:

X_smaller = ABC/[AC + BC - AB + 2√ABC(C-A-B)]
X_larger = ABC/[AC + BC - AB - 2√ABC(C-A-B)]

If A + B = C, the two solutions are equal.

Example: Two tangent circles with radii of 4 and 9 are tangent to and inside of a circle with a radius of 49. Using the formulas above, we have:

X_smaller = 1764/[196 + 441 - 36 + 2√1764*36]
= 1764/(601 + 2*252)
= 1764/1105
= 1.59638

X_larger = 1764/[196 + 441 - 36 - 2√1764*36]
= 1764/(601 - 2*252)
= 1764/97
= 18.18557

© Had2Know 2010