Triangle Bounded by 3 Lines

Given three mutually non-parallel lines in the xy coordinate plane, those lines will either intersect at a common point, or intersect pairwise in three distinct points and form the boundary of a triangle.



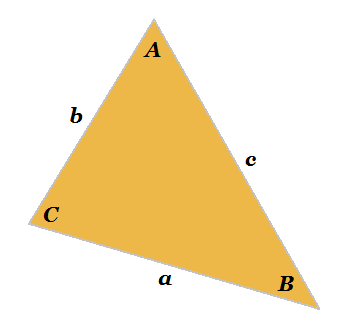
To determine the area, perimeter, and angles of this triangle you must first solve for the intersection points. Then, once you know the three points that define the vertices of the triangle, you can either use vector algebra or a solver to find the side and angle measures and the area. To use the calculator on the left, input the equations of the three lines in standard form ax + by = c. The calculator will output the coordinates of the vertices, angles, sides, area, and perimeter.

© Had2Know 2010