Measuring Observed Angles Without a Protractor

Using Trigonometric Functions to Evaluate Angles

If you don't have a protractor to find the degree measure of an angle, you can use trigonometry to evaluate the angle. The key is to think of the angle as part of a right triangle. Using the inverse operations for sine, cosine, or tangent, you can calculate the angle from the side lengths of the right triangle. All you need is a hand calculator with trig functions.

For example, suppose a ramp connects the front porch of a house to the sidewalk. The horizontal distance between one end of the ramp and the other forms one leg of a right triangle; the height of the porch forms the other leg. The total length of the ramp itself forms the hypotenuse of this right triangle.

Since the tangent of an angle is rise over run, the angle of the ramp is

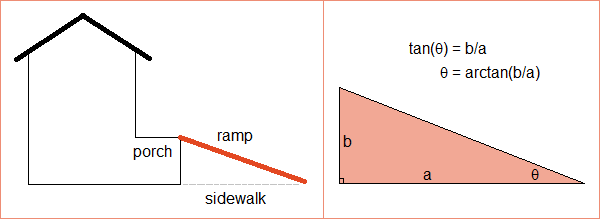
tan^-1(rise/run).

(Note tan^-1 is an alternative notation for arctan.) If the height is 1 foot and the horizontal distance is 5.5 feet, then the angle is tan^-1(1/5.5) = 10.3°.

Another way to calculate the angle of inclination is with the height and hypotenuse. Since the sine of an angle is rise over hypotenuse, the angle of the ramp can also be expressed as sin^-1(rise/hypotenuse).

Yet a third way is with cosine. The cosine of an angle is the run over hypotenuse, so the angle equals cos^-1(run/hypotenuse).

Pythagorean Theorem and Formula Review

If you know any two sides of a right triangle, you can compute the third with the Pythagorean Theorem. If A and B are two legs of the right triangle and C is the hypotenuse, then

C² = A² + B², or
C = √A² + B².

Here is a summary of the angle formulas:

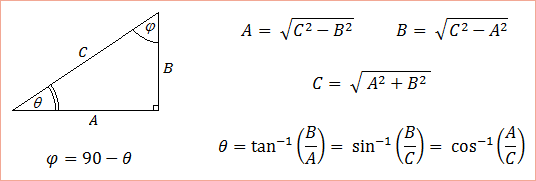
© Had2Know 2010