Copyright © Had2Know 2010-2026. All Rights Reserved.
Terms of Use | Privacy Policy | Contact
Site Design by E. Emerson
Constructing Geometric Solids:
Rhombic Triacontahedron
A rhombic triacontahedron is a 30-sided solid figure with all rhombic faces. In geometry, a rhombus is a quadrilateral whose four sides have equal length. The rhombic triacontahedron is the dual of the icosidodecahedron (polyhedron with 12 pentagonal faces and 20 triangular faces), since each vertex of the rhombic triacontahedron corresponds to a face of the icosidodecahedron and vice versa.
You can use cardstock and tape to construct a rhombic triacontahedron using the pattern and instructions below. You will need a ruler and pencil to measure the precise shape of the rhombic faces, and sharp scissors or an Xacto knife to cut out the pattern.
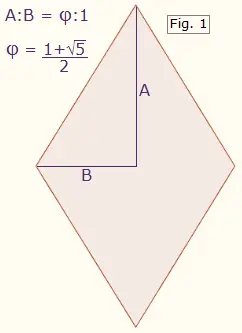
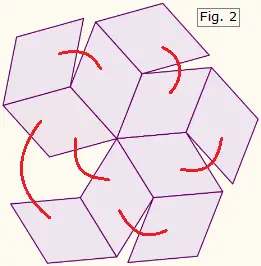
Using a sharp pencil and ruler, draw two copies of Figure 2 below. Cut out each figure and fold all of the lines in the same direction, toward you, so that the figure curls into itself. Tape the edges together as indicated by the red arcs. The result will be two bowl-shaped components with 10 facets apiece.
Next, draw and cut the shape in Figure 3. Fold all of the edges in the same direction and tape the ends together where indicated by the red lines. The result will be a ring-shaped figure with ten facets.

You now have two bowls and a ring. To assemble the rhombic triacontahedron, tape one of the bowls to the top of the ring, and the other bowl to the bottom of the ring. You can also cut tabs on the ring and glue them under the edges of each bowl.
© Had2Know 2010
