Ellipse Approximation: Method 1

Finding two circular arcs whose normal line at the intersection point is perpendicular to the diagonal connecting the top and side of the pseudo-ellipse

For many practical applications, it is easier to create approximations of ellipses rather than true ellipses. Pairs of circular arcs can be joined at a point of tangency to make smooth pseudo-ellipses. There is some freedom in choosing the radii of the arcs to form a pseudo-ellipse with given major and minor axis lengths.

For example, you can choose the radii such that the arcs are quarter circles. Or, as explained in this article, you can choose the radii such that the normal line XC₂ and the diagonal AB are perpendicular. See diagram below for more detail.

Here, a and b are the half-lengths of the major and minor axes respectively. The lengths r₂ and r₁ are the radii of the larger and smaller circular arcs respectively. The points C₂ and C₁ are the respective centers of these circles. X is the point where the two circular arcs meet tangently, and the points X, C₁, and C₂ are collinear.

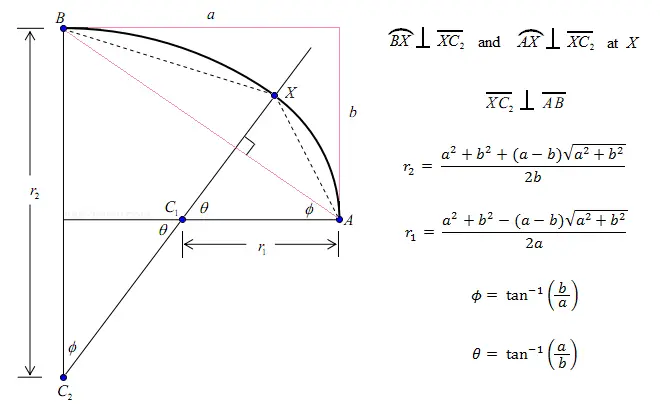
By using the right triangle relation leg² + leg² = hypotenuse², you can find the values of r₂ and r₁ in terms of a and b. This formula is shown in the figure above. The angles of the arcs, φ and θ can be determined once you know r₂ and r₁.

Example: Suppose you want to make an ellipse approximation that is 8 inches long and 6 inches wide. Thus, a = 4 and b = 3. Using the formula above, you can compute

r₂ = [16 + 9 + 1*sqrt(25)]/[2*3]
= [25 + 5]/6
= 5

r₁ = [16 + 9 - 1*sqrt(25)]/[2*4]
= [25 - 5]/8
= 2.5

The angles of these arcs are

φ = arctan(3/4) = 36.87°

θ = arctan(4/3) = 53.13°

© Had2Know 2010