Copyright © Had2Know 2010-2025. All Rights Reserved.
Terms of Use | Privacy Policy | Contact
Site Design by E. Emerson
How to Find the Great Circle Distance Between Two Points on a Sphere
On a sphere, the shortest path connecting two points lies on a great circle, a circumference circle on the sphere. Sometimes the shortest arc length between two points on a sphere is called the great circle distance. In 3-dimensional space, you can compute the spherical distance between two points if you know the points' Cartesian coordinates and the radius of the sphere.
You can apply the equations below, or use the spherical distance calculator on the left. If you want to compute the distance between two cities using latitude and longitude, see the City Distance Calculator instead. For that calculator, you only need to input the latitude/longitude of each location.
Spherical Distance Formula
If the coordinates of the two points are (a, b, c) and (d, e, f) and the radius of the sphere is r, then the arc length between the two points is given by the equationArc = 2r*sin-1(w/(2r)),
where w = √((a-d)² + (b-e)² + (c-f)²), i.e., the linear distance between the two points. The output of the inverse sine function, sin-1, is in radians. So long as w is not greater than 2r, the formula will give you the great circle distance between the two coordinates. If w exceeds 2r, the distance between the points exceeds the diameter of the sphere.
Justification
The formula for spherical distance follows from the formula for arc length in terms of the radius and chord length. For a circle with a radius of r and a chord segment length of w, the angle of the section isθ = 2sin-1(w/(2r)).
The arc length is r times θ. See figure below:
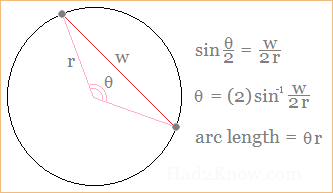
© Had2Know 2010
