How to Compute Put/Call Prices with the Black-Scholes Formula

The prices of puts and calls in the European options market can be computed with the Black-Scholes model. The Black-Scholes call/put price formula is the solution to the partial differential equation



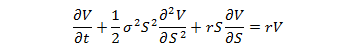
where V(S,t) is the value of the option, S is the share price, t is time in years, r is the risk-free rate of return, σ is the volatility, and K is the strike price. With different boundary conditions of V(S,t), you get either the value of a call option C(S,t) or the value of a put option P(S,t):

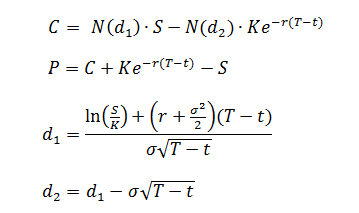
In the formulas above, T-t is the time to maturity in years and the function N(x) is the cumulative normal distribution function. N(x) is related to the error function erf(x) by the expression

N(x) = ½ + ½erf(x/√2)

Because the call and put functions are difficult to evaluate by hand or with a simple hand calculator, more sophisticated tools are used, such as the calculator above.

Assumptions Used in Black-Scholes Pricing

The Black-Scholes model is not a perfect model for predicting the prices of puts and calls because it relies on several assumptions that may not match the reality of options trading. For example, the Black-Scholes model is only valid for European options, which can only be exercised on the expiration date. American options can be exercised any time before the expiration date, which invalidates the Black-Scholes equation. The other assumptions behind the model are

(1) constant volatility
(2) no dividends
(3) no arbitrage
(4) borrowing and lending money at a known and constant risk-free interest rate is possible
(5) no transaction fees

Despite some limitations, the Black-Scholes model is still useful for calculating the approximate prices of options.

Volatility in Black-Scholes Pricing

The volatility used in the Black-Scholes pricing model is the standard deviation of the logarithmic returns.

© Had2Know 2010